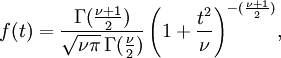Lecture 8 - Confidence Interval for Ŷ

Confidence Interval for Ŷ
Once we've calculated our regression coefficients, b₀ and b₁, we can estimate the value of Y at any given X with the formula:
Ŷ = b₀ + b₁X

This is known as a point estimate. It estimates Ŷ to a point. However, since it's just an estimate, it's logical to ask for a confidence interval around Ŷ.

In addition to constructing a confidence interval for an individual Ŷ, we can also construct a confidence interval for an average Ŷ at X.

The difference is best illustrated with an example. In site.mtw we have data on square footage of stores and their annual sales. In general, sales increase linearly with increasing square footage. We perform a regression analysis and determine the regression coefficients. Now we could ask two questions:
1. If I build a single new store with 4,000 square feet, what does the regression predict for its annual sales? The answer can be expressed as a confidence interval for an individual Ŷ, because we're making a prediction for an individual new store.
2. If I build 10 new stores, each with 4,000 square feet, what does the regression predict for the average annual sales of those stores? The answer to this question can be expressed as a confidence interval for an average Ŷ, since we're making a prediction about the average sales at many new stores.

Confidence Interval for Average Ŷ
The confidence interval for the average Ŷ (question #2 above) takes the common form:where S_Ŷ is the standard error of Ŷ. Note: n-2 is used in looking up the t value in the t table.

We are told thatwhere h_i is given by:
That's all there is to it! Well see in a minute that Minitab can calculate the standard error term for us, so it's constructing the interval is just a matter of looking up the value in the t table and then doing the arithmetic.

Confidence Interval for Individual Ŷ
If we're constructing the confidence interval for an individual Ŷ (question #1 above), the calculations are very similar except that we use a 1+h_i term in place of h_i. So that term becomes:Other than the standard error term, everything else is the same as calculating for an average Ŷ.

Using Minitab to calculate the confidence interval
Here's how to get the info we need out of Minitab:
1. Load up your data in a worksheet. (We use the site.mtw file as usual.)
2. Select Stat-Regression-Regression from the menubar.
3. Put the independent variable (square feet) in the Predictor box. Put the dependent variable (annual sales) in the Response box.
4. Click the Options button. Enter 4 in the Prediction interval for new observations box. This tells Minitab that we want a prediction of annual sales at 4000 square feet (the units of our data are thousands of feet).
5. Check the Confidence Limit checkbox if you want a confidence interval for an average Y. Check the Prediction Limit checkbox if you want a confidence interval for an individual Y.
6. Click OK in the Options and the main Regression windows. The results appear in the session window. Here's the relevant information:

Predicted Values for New Observations

New
Obs    Fit  SE Fit      95% CI          95% PI
  1  7.644   0.309  (6.971, 8.317)  (5.433, 9.854)

The prediction is 7.64 (the "fit"). The SE Fit term is the standard error for the average Y (the one with just h_i, not 1+h_i.

I suspect that we'll probably be expected to construct the confidence interval for the average Y, given the Fit and SE Fit output. Don't forget: You still need to look up the t value (at n-2!) and multiply the SE Fit value by it.

Lecture 8 - Inferences About the Regression Slope - Part 2

Confidence Interval for b₁
The second question that we ask when evaluating the regression is: What is the confidence interval for b₁?

Like any confidence interval, this one will take the form:
b₁ ± t_{α/2, n-2} S_b1

In the last blog post, we found that S_b1 is:
S_b1 = S_XY/SQRT(SSX)

Knowing S_b1, we can look up t in the t-table and construct the confidence interval relatively easily.

Note that for the confidence interval for b₁ we use n-2 in looking up the t-score.

Using Minitab to evaluate the regression
We won't be expected to calculate S_XY and S_b1 by hand for the final (or so we were told). But we will likely be asked to create a confidence interval for b₁ given a snippet of Minitab output. So it's worthwhile to take a look at it:

We used the site.mtw dataset and ran the standard regression analysis and got this:

Predictor      Coef  SE Coef      T      P
Constant     0.9645   0.5262   1.83  0.092
Square Feet  1.6699   0.1569  10.64  0.000
S = 0.966380   R-Sq = 90.4%   R-Sq(adj) = 89.6%

The S_b1 value is calculated for us, but it's not obvious where it is. It's the SE Coef term that I've highlighted in red. b₁ itself is the Coef term, in blue. With those two numbers and a t-table, you can construct a confidence interval for b₁. Just remember to use n-2 in the t-table.

With these two values you can also determine the t statistic for hypothesis testing β₁=0 from the previous blog post by dividing b₁/S_b1. But the truth is, you don't have to do that! The t-value for b₁ is right there in the Minitab output also. I've highlighted it in green. The number in the p column (highlighted purple) is the p-value for b₁. So if that number is less than α/2, then you can reject the hypothesis that β₀ is 0.

Lecture 8 - Inferences About the Regression Slope

After we use the method of least-squares to calculate regression coefficients (b₀ and b₁) and we validate the LINE assumptions, we next turn to evaluating the regression, specifically the slope, b₁ and ask two questions:
1. Is it statistically significant?
2. What is the confidence interval for b₁?

The first question (we actually covered this after the second question in class), whether b₁ is statistically significant, is determined by asking: Is it any better than a flat horizontal line through the data?

We answer this question by making a hypothesis that the true relationship slope, β₁ is 0 and using our skills at hypothesis testing to determine whether we should reject that hypothesis.

H₀: β₁ = 0
H₁: β₁ ≠ 0

The t statistic that we use to test the hypothesis is:
t = (b₁-β₁)/S_b1
where S_b1 is the standard error of the slope.

In our case, β₁ is 0 according to our hypothesis, so t reduces to:
t = b₁/S_b1

The standard error of the slope, S_b1, is defined as:
S_b1 = S_XY/SQRT(SSX)
where S_XY is the standard error of the estimate.

The standard error of the estimate, S_XY, is defined as:
S_XY = SQRT(SSE/n-2)

So, if we have our calculations of SSX and SSE, we can do the math and find S_b1 and the t-score for b₁.

We finish our hypothesis testing by comparing the t-score for b₁ to t_{α/2, n-2}, where α is our level of significance.
If t is beyond t_{α/2, n-2} (either on the positive or negative end), we conclude that the hypothesis, H₀, must be rejected.
We could also make the conclusion based on the p-value of the t-score. If the p-value is less than α/2, then we reject H₀.

**Confidence interval for b₁ will be covered in the next blog post.**

Lecture 8 - Residual Analysis - Checking Independence of Errors

Checking the Independence of Errors Assumption
The "I" in the LINE mnemonic stands for Independence of Errors. This means that the distribution of errors is random and not influenced by or correlated to the errors in prior observations. The opposite is independence is called autocorrelation.

Clearly, we can only check for independence/autocorrelation when we know the order in which the observations were made and the data points were collected.

We check for independence/autocorrelation in two ways. First, we can plot the residuals vs. the sequential number of the data point. If we notice a pattern, we say that there is an autocorrelation effect among the residuals and the independence assumption is not valid. The plot at right of residuals vs. observation week shows a clear up and down pattern of the residuals and indicates that the residuals are not independent.

The second test of independent/autocorrelation is a more quantitative measure. (All the methods that we've used up to this point for checking assumptions have been graphical/visual.) This test involves calculating the Durbin-Watson Statistic. The D-W statistic is defined as:
It's the sum of the squares of the differences between consecutive errors divided by the the sum of the squares of all errors.

Another way to look at the Durbin-Watson Statistic is:

D = 2(1-ρ)

where ρ (the Greek letter rho - lower case) = the correlation between consecutive errors.

Looking at it that way, there are 3 important values for D:
D=0: This means that ρ=1, indicating a positive correlation.
D=2: In this case, ρ=0, indicating no correlation.
D=4: ρ=-1, indicating a negative correlation

In order to assess whether there is independence, we check to see if D is close to 2 (in which case we say there is no correlation and errors are independent) or if it's closer to one of the other extreme values of 0 or 4 (in which case we say that the independence assumption is not valid). There is also some grey area between both 0 and 2 and between 2 and 4 in which case we say that the Durbin-Watson statistic does not give us enough information to make a determination, it is inconclusive.

To determine the boundaries for when the Durbin-Watson statistic is relevant and when it's inconclusive, we turn to table E.9, which provides us with lower and upper bounds, d_L and d_U.

Reading the Durbin-Watson Critical Values Table
The critical values are dependent on the sample size, n, the number of independent variables in the regression model, k, and the level of significance, α. In the case of simple linear regression, there's always only 1 independent variable. (That's the simple part.) The level of significance is usually 0.01 (99% confidence) or 0.05 (95% confidence).

So, to read the table:
1. Locate the large section of the table for your level of significance, α.
2. Find the two columns, d_L and d_U, for k=1 (assuming it's simple).
3. Go down the column to the row with your sample size, n.
4. Read the two values for d_L and d_U

Interpreting the Durbin-Watson Statistic
0 < D < d_L: There is positive autocorrelation
d_L < D < d_U: Inconclusive
d_U < D < 2+d_L: No autocorrelation
2+d_L < D < 2+d_U: Inconclusive
2+d_U < D < 4: There is negative autocorrelation

Graphically, it can be represented like this:

Note: Positive autocorrelation is somewhat common. Negative autocorrelation is very uncommon and our book does not deal with it.

Lecture 8 - Residual Analysis - Checking the Equal Variance Assumption

Homoscadasticity (Not that there's anything wrong with that.)
We now turn to checking the assumption of equal variance of errors, the "E" in our LINE mnemonic. This assumptions states that not only is the error at each x-value distributed normally, but the variance in the error is equal at each point.

Equal variance of errors is known as homoscadasticity. Unequal variance of errors is called heteroscadasticity.

For this analysis we turn again to the plot of residuals vs. the independent variable (x) that we used in when we validated the linearity assumption. For linearity, we were just looking to see if the residuals were evenly distributed above and below the x-axis. To check for equal variance of errors, we check to see if there's any pattern in the distribution of the residuals around the x-axis.

Running the residual plot versus x in Minitab:
1. Load up your data.
2. Select Stat-Regression-Regression from the menu bar.
3. Put Annual Sales in the Response box and Square Feet in the Predictor box.
4. Click the Graphs button. Put Square Feet in the Residuals versus the variables box.
5. Click OK in both the Graphs and Regression dialogs. The residual plot appears.

Review the graph and ask yourself: Is there any pattern in the residuals? Do they get increasing larger or small as x changes? If so, then you have a case of heteroscadasticity. But if the residuals are distributed evenly and consistently around the x-axis, then you can conclude that the variances are consistent and the assumption of equality of variances is valid.

In our example, I'd be somewhat concerned with the fact that the residuals are closer to the x-axis for small values of x, but broaden out for larger values. The variance does seem to taper off as x gets very large, which is an indication that the variances are equal for x>2 or so. (Click the graph for a larger view of the plot.)

Lecture 8 - Residual Analysis - Checking the Normality Assumption

The next assumption in the LINE mnemonic after Linearity is Independence of Errors. We skipped that one momentarily because it's a bit more complex than the others. So we saved it for last. In the meantime, we looked at the next assumption: Normality of Error.

Checking the Normality Assumption
This assumption states that the error in the observation is distributed normally at each x-value. A larger error is less likely than a smaller error and the distribution of errors at any x follows the normal distribution.

Although we typically only have one observation at each x, if we assume that the distribution of the errors is the same at each x, we can simply plot all the errors (residuals) and check if they follow the normal distribution. We do this by running a normal probability plot of the residuals. Fortunately for us, Minitab has a built-in normal probability plot function.

Checking Normality Using Minitab
1. Open up your data worksheet. As usual, we'll use the site.mtw file for our example.
2. Select Stat-Regression-Regression from the menu bar.
3. Put Annual Sales in the Response box since it's the dependent (response) variable and put Square Feet in the Predictors box since it's the independent (predictor) variable.
4. Click the Graph button and under Residual Plots, check the Normal plot of residuals checkbox.
5. Click OK in the Graphs and the Regression dialogs.

Minitab creates the normal probability plot of the residuals. The y-axis of this graph is adjusted so that if the data are distributed normally, they will fall on a straight line on the graph. Minitab even draws a line through the residuals for us (presumably using the method of least-squares).

Drawing a conclusion from the graph
Review this graph and ask yourself: Do the residual points fall more-or-less on a straight line in the normal probability plot? If they do, you can conclude that the errors are distributed normally and the normality of errors assumption is valid. In our example, the normality plot of the residuals are pretty much linear, but I would be concerned about the upward trend at the far right end of the graph. (Click the graph to see it in more detail.)

Lecture 8 - Residual Analysis - Checking Linearity

Checking Linearity
Our method for checking the first assumption, linearity of the data, is not a precise, quantitative test. Rather, we'll use visual inspection to check for linearity.

One quick way to test the linearity of the data is to create an x-y scatter plot and observe whether the data generally follows a straight line (either with positive or negative slope). Plotting the regression line through the data may help visualize this as well.

Using Minitab for the linearity check:
1. Bring up your data in a worksheet. We used the site.mtw file in class.
2. Select Graph-Scatterplot from the menu bar. Select the "With Regression" option when prompted for the type of scatterplot.
3. Put Annual Sales (the dependent variable) in the Y Variables column and Square Feet (the independent variable) in the X Variables column. Remember that the independent variable is the variable that you can control and which you think will be a predictor of the dependent variable. In other words, the annual sales is dependent on the size of the store (in square feet). It's not the other way around. The size of the store doesn't grow or shrink depending on the number of sales!
4. Don't change the default options and click OK. You should get a plot of your data with a regression line through it. (If you don't get the regression line, in step 3 click Data View, Regression Tab and make sure Linear is selected.)

To interpret the linearity of this graph, "eyeball" the way the points fall above and below the regression line and ask yourself: Are the data points relatively linear or is it curved or skewed in some way? In our case, the data is relatively linear and not curved, so we conclude that the assumption of linearity is valid.

A better way to visually assess the linearity is to plot the residuals versus the independent variable and look to see if the errors are distributed evenly above and below 0 along the entire length of the sample.

Plotting Residuals versus the Independent Variable with Minitab
1. Select Stat-Regression from the menu bar.
2. Put Annual Sales in the Response box and Square Feet in the Predictors box. In our scenario, we think that the number of square feet will be a predictor of the annual sales of the store. Notice that the predictors box is large. There can be more than one predictor - perhaps advertising, employee training, etc. Many things can influence the response variable - the annual sales. We'll get to that during multiple linear regression. Right now, for simple linear regression, we're just looking at a single predictor.
3. Click the Graphs button. Put Square Feet in the Residuals versus the variables box.

To interpret this graph, ask yourself: Do the residual points fall equally above and below 0 along the entire length of the horizontal axis? In our case, the residuals do more or less fall equally above and below 0, so we conclude that the data is linear and the assumption of linearity is valid. Note: We also see that the residuals are closer to 0 for lower values of x (square feet). That may become important later when we talk about equal variance of errors.

Lecture 8 - Residual Analysis - Definition

Residual Analysis
In Lecture 7 we discussed how to use the method of least-square to perform simple linear regression on a set of data. We also discussed the four assumptions we make about our data in order to use the method of least-squares for the regression:
1. Linearity
2. Independence of errors
3. Normality of error
4. Equal variance of errors

The error is also known as the residual and is the difference between the observed Y_i value, for any particular X_i, and the value for Y_i predicted by our regression model which is usually symbolized by Ŷ_i (read "y hat sub i"). The residual is symbolized by the greek letter epsilon (lower case) - ε_i.

ε_i = Y_i - Ŷ_i

We perform a four-part residual analysis on our data to evaluate whether each of the four assumptions hold and, based on the outcome, we can determine whether our linear regression model is the correct model.

It's called a residual analysis because 3 of the 4 assumptions (independence, normality and equality of variance) directly relate to the errors (the residuals) and the other assumption (linearity) is tested by assessing the residuals.

Lecture 7 - Coefficient of Determination

After calculating β₀ and β₁ to determine the best line to fit the data, we want to quantify how well the line fits the data. It may be the best line, but how good is it?

Sum of Squares
Looking at the graph of the data, we could say that without any modeling or regression at all, we would expect the y-value for any give x to be the mean y, ybar. Most of the observations, of course, would not be equal to the mean. We can measure how far the observations are from the mean by taking the difference between each y_i and ybar, squaring them, and taking the sum of the squares. We call this the total sum of squares or SST.

You probably remember that the variance that we discussed much earlier in the course is this sum of squares divided by n-1.

The total sum of squares is made up of two parts - the part that is explained by the regression (yhat-ybar) and the part that the observation differs from the regression (y_i-yhat). When we square each of these and sum them we compute the regression sum of squares, SSR, and the error sum of squares, SSE.

Coefficient of Determination
The 3 sum of squares terms, SST, SSR and SSE, don't tell us much by themselves. If we're dealing with observations which use large units, these terms may be relatively large even though the variance from a linear relationship is small. On the other hand, if the units of the measurements in our observations is small, the sum of square terms may be small even when the variance from linearity is great.

Therefore, the objective statistic that we use to assess how well the regression fits the data is the ratio of the regression sum of squares, SSR, to the total sum of squares, SST. We call this statistic the coefficient of determination, r².

r² = SSR / SST

Lecture 7 - Assumptions in the Method of Least Squares

Photo courtesy of F. Espenak at MrEclipse.com

Assumptions
In order to use the Least Squares Method, we must make 4 fundamental assumptions about our data and the underlying relationship between the independent and dependent variables, x and y.

1. Linearity - that the variables are truly related to each other in a linear relationship.
2. Independence - that the errors in the observations are independent from one another.
3. Normality - that the errors in the observations are distributed normally at each x-value. A larger error is less likely than a smaller error and the distribution of errors at any x follows the normal distribution.
4. Equal variance - that the distribution of errors at each x (which is normal as in #3 above) has the identical variance. Errors are not more widely distributed at different x-values.

A useful mnemonic device for remembering these assumptions is the word LINE - Linearity, Independence, Normality, Equal variance.

Note that the first assumption, linearity, refers to the true relationship between the variables. The other three assumptions refer to the nature of the errors in the observed values for the dependent variable.

If these assumptions are not true, we need to use a different method to perform the linear regression.

The Least-Squares Method

The Method of Least Squares
As described in the previous post, the least-squares method minimizes the sum of the squares of the error between the y-values estimated by the model and the observed y-values.

In mathematical terms, we need to minimize the following:
∑ (y_i - (β₀+β₁x_i))

All the y_i and x_i are known and constant, so this can be looked at as a function of β₀ and β₁. We need to find the β₀ and β₁ that minimize the total sum.

From calculus we remember that to minimize a function, we take the derivative of the function, set it to zero and solve. Since this is a function of two variables, we take two derivatives - the partial derivative with respect to β₀ and the partial derivative with respect to β₁.

Don't worry! We won't need to do any of this in practice - it's all been done years ago and the generalized solutions are well know.

To find b₀ and b₁:
1. Calculate xbar and ybar, the mean values for x and y.
2. Calculate the difference between each x and xbar. Call it xdiff.
3. Calculate the difference between each y and ybar. Call it ydiff.
4. b1 = [∑(xdiff)(ydiff)] / ∑(xdiff²)
5. b₀ = ybar - b₁xbar

Notice that we switched from using β to using b? That's because β is used for the regression coefficients of the actual linear relationship. b is used to represent our estimate of the coefficients determined by the least squares method. We may or may not be correctly estimating β with our b. We can only hope!

Lecture 7 - Simple Linear Regression

Linear Regression essentially means creating a linear model that describes the relationship between two variables.

Our type of linear regression is often referred to as simple linear regression. The simple part of the linear regression refers to the fact that we don't consider other factors in the relationship - just the two variables. When we model how several variables may determine another variable, it's called multiple regression - the topic for a more advanced course (or chapter 13 in our text).

For example, we may think that the total sales at various stores is proportional to the number of square feet of space in the store. If we collect data from a number of stores and plot them in an XY scatter plot, we would probably find that the data points don't lie on a perfectly straight line. However, they may be "more or less" linear to the naked eye. Linear regression involves finding a single line that approximates the relationship. With this line, we can estimate the expected sales at a new store, given the number of square feet it will have.

In mathematical terms, linear regression means finding values for β₀ and β₁ in the equation

y = β₀ + β₁x

such that the resulting equation fits the data points as closely as possible.

The equation above may look more familiar to you in this form:

y = mx + b

That's the form we learned in linear algebra. m is the slope and b is the y-intercept. Similarly, in our statistical form, β₁ is the slope and β₀ is the y-intercept.

How Close is Close?
We said that we want to find a line that fits the data "as closely as possible". How close is that? Well, for any given β₀ and β₁, we can calculate how for off we are by looking at each x-value, calculating what the linear estimate would be according to our regression equation and comparing that to the actual observed y-value. The difference is error between our regression estimate and the observation. Clearly, we want to find the line that minimizes the total error.

Minimizing the total error is done in practice by minimizing the sum of the squares of the errors. If we used the actual error term, and not the square, positive and negative errors would cancel each other out. We don't use the absolute value of the error term because we will need to integrate it and the absolute value function is not integrable at 0.

Generating regression coefficients β₀ and β₁ for the linear model by minimizing the sum of the square of the errors is known as the least-squares method.

Lecture 7 - Using Minitab to Calculate Hypothesis Testing Statistics

Using Minitab to Calculate Hypothesis Testing Statistics
Minitab can be used to perform some of the calculations that are required in steps 4 and 5 of the critical value approach and step 4 of the p-value approach to hypothesis testing (see previous 2 posts). You still need to do all the study design in steps 1-3 and use them as input to Minitab. You will also need to draw your own conclusions from the calculations that Minitab performs.

Here's how:
1. Load up your data in a Minitab worksheet. (In lecture 7, we used the data in the insurance.mtw worksheet from exercise 9.59.)
2. Select Stat - Basic Statistics from the menu bar. Since we're doing hypothesis testing of the mean, we have 2 choices from the menu. Either "1-sample z" or "1-sample t". Since we don't know the standard deviation of the population, we choose the "1-sample t" test.
3. In the dialog box, select the column that has your sample data and click the select button so it appears in the "Samples in columns" box. In the test mean box, enter the historical value for the mean, which in our case is 45.
4. Click the Options button and enter the confidence level ((1-&alpha)x100) and select a testing "alternative". The testing alternative is where you specify the testing condition of the alternative hypothesis.

• If H₁ states that the mean is not equal to the historical value, select not equal. Minitab will make calculations for a two-tail test.
• If H₁ states that the mean is strictly less than or strictly greater than the historical value, select less than or greater than. In this case, Minitab will calculate values for a one-tail test.

5. Click Ok in the Options dialog and Ok in the main dialog. Minitab displays the calculated values in the Session window. The results from our sample data looked like this:

One-Sample T: Time
Test of mu = 45 vs not = 45

Variable N  Mean    StDev  SE Mean       95% CI        T    P
Time     27 43.8889 25.2835 4.8658 (33.8871, 53.8907) -0.23 0.821

Unfortunately, Minitab doesn't take the hypothesis testing all the way to drawing a conclusion about the null hypothesis. We need to do that ourselves in one of two ways: either the critical value or p-value approach.

For the critical value approach, we need to additionally look up the t-score for t_0.025,26 = ±2.056. 0.025 is α/2, which we use with this two-tail test. 26 is n-1, the degrees of freedom for this test. We compare t_0.025,26 to the t-score of the sample mean, which Minitab calculated for us as -0.23, and find that the t-score of the sample mean is between the critical values and therefore we do not reject H₀.

For the p-value approach, we compare the p-value that Minitab calculated as 0.821 and compare that to the level of significance, &alpha, which in our case is 0.10. Since the p-value is larger than α we do not reject H₀.

Hypothesis Testing - p-Value Approach - 5 Step Methodology

The p-Value Approach
The p-value approach to hypothesis testing is very similar to the critical value approach (see previous post). Rather than deciding whether or not to reject the null hypothesis based on whether the test statistic falls in a rejection region or not, the p-value approach allows us to make the decision based on whether or not the p-value of the sample data is more or less than the level of confidence.

The p-value is the probability of getting a test statistic equal to or more extreme than the sample result. If the p-value is greater than the level of confidence then we can say that the probability of a more extreme test statistic is larger than the level of confidence and thus we do not reject H₀.

If, on the other hand, the p-value is less than the level of confidence, we conclude that the probability of a more extreme test statistic is smaller than the level of confidence and thus we reject H₀.

The five step methodology of the p-value approach to hypothesis testing is as follows:
(Note: The first three steps are identical to the critical value approach described in the previous post. However, step 4, the calculation of the critical value, is omitted in this method. Differences in the final two steps between the critical value approach and the p-value approach are emphasized.)

State the Hypotheses
1. State the null hypothesis, H₀, and the alternative hypothesis, H₁.
Design the Study
2. Choose the level of significance, α according to the importance of the risk or committing Type I errors. Determine the sample size, n, based on the resources available to collect the data.
3. Determine the test statistic and sampling distribution. When the hypotheses involve the population mean, μ, the test statistic is z when σ is known and t when σ is not known. These test statistics follow the normal distribution and the t-distribution respectively.
Conduct the Study
4. Collect the data and compute the test statistic and the p-value.
Draw Conclusions
5. Evaluate the p-value and determine whether or not to reject the null hypothesis. Summarize the results and state a managerial conclusion in the context of the problem.

Example (we'll look at the same example as the last post, also reviewed at the beginning of Lecture 7):
A phone industry manager thinks that customer monthly cell phone bills have increased and now average over $52 per month. The company asks you to test this claim. The population standard deviation, σ, is known to be equal to 10 from historical data.

The Hypotheses
1.H₀: μ ≤ 52
H₁: μ > 52
Study Design
2. After consulting with the manager and discussing error risk, we choose a level of significance, α, of 0.10. Our resources allow us to sample 64 sample cell phone bills.
3. Since our hypothesis involves the population mean and we know the population standard deviation, our test statistic is z and follows the normal distribution.
The Study
4. We conduct our study and find that the mean of the 64 sample cell phone bills is 53.1. We compute the test statstic, z = (xbar-μ)/(σ/√n) = (53.1-52)/(10/√64) = 0.88. Next, we look up the p-value of 0.88. The cumulative normal distribution table tells us that the area to the left of 0.88 is 0.8106. Therefore, the p-value of 0.88 = 1-0.8106 = 0.1894.
Conclusions
5. Since 0.1894 is greater than the level of significance, α, we do not reject the null hypothesis. We report to the company that, based on our testing, there is not evidence that the mean cell phone bill has increased from $52 per month.

Hypothesis Testing - Critical Value Approach - 6 Step Methodology

The six-step methodology of the Critical Value Approach to hypothesis testing is as follows:
(Note: The methodology below works equally well for both one-tail and two-tail hypothesis testing.)

State the Hypotheses
1. State the null hypothesis, H₀, and the alternative hypothesis, H₁.
Design the Study
2. Choose the level of significance, α according to the importance of the risk or committing Type I errors. Determine the sample size, n, based on the resources available to collect the data.
3. Determine the test statistic and sampling distribution. When the hypotheses involve the population mean, μ, the test statistic is z when σ is known and t when σ is not known. These test statistics follow the normal distribution and the t-distribution respectively.
4. Determine the critical values that divide the rejection and non-rejection regions.
Note: For ethical reasons, the level of significance and critical values should be determined prior to conducting the test. The test should be designed so that the predetermined values do not influence the test results.
Conduct the Study
5. Collect the data and compute the test statistic.
Draw Conclusions
6. Evaluate the test statistic and determine whether or not to reject the null hypothesis. Summarize the results and state a managerial conclusion in the context of the problem.

Example (reviewed at the beginning of Lecture 7):
A phone industry manager thinks that customer monthly cell phone bills have increased and now average over $52 per month. The company asks you to test this claim. The population standard deviation, σ, is known to be equal to 10 from historical data.

The Hypotheses
1.H₀: μ ≤ 52
H₁: μ > 52
Study Design
2. After consulting with the manager and discussing error risk, we choose a level of significance, α, of 0.10. Our resources allow us to sample 64 sample cell phone bills.
3. Since our hypothesis involves the population mean and we know the population standard deviation, our test statistic is z and follows the normal distribution.
4. In determining the critical value, we first recognize this test as a one-tail test since the null hypothesis involves an inequality, ≤. Therefore the rejection region is entirely on the side of the distribution greater than the historic mean - right tail.
We want to determine a z-value for which the area to the right of that value is 0.10, our α. We can use the cumulative normal distribution table (which gives areas to the left of the z-value) and find z having value 0.90 = 1.285. This is our critical value.
The Study
5. We conduct our study and find that the mean of the 64 sample cell phone bills is 53.1. We compute the test statstic, z = (xbar-μ)/(σ/√n) = (53.1-52)/(10/√64) = 0.88.
Conclusions
6. Since 0.88 is less than the critical value of 1.285, we do not reject the null hypothesis. We report to the company that, based on our testing, there is not evidence that the mean cell phone bill has increased from $52 per month.

Lecture 6 - Ch 9b - One-Tail Hypothesis Testing

When the null hypothesis is that the current population mean equals the historic mean and the alternative hypothesis is that it does not equal the historic mean, we construct a two-tailed rejection region on either side of the distribution. We reject H₀ is the sample mean is too high to too low.

However, that's not always the case. Sometimes, our null hypothesis is that the mean is at least equal to the historic mean (but possibly larger). In such a case, we would only reject H₀ if it was less than the lower bound (critical value) of the non-rejection region.




Similarly, sometimes our H₀ is that the mean is at most equal to the historic mean (but possibly smaller). In this a case, we would only reject H₀ if it was greater than the lower bound (critical value) of the non-rejection region.

The methodology for doing a one-tail hypothesis test is almost the same as for the two-tail test. The major difference is that our entire rejection region is on one side of the distribution. Therefore, when you set the level of significance, alpha, and the confidence level, (1-alpha)x100, that reflects only one side of the distribution.

Practically speaking, it means that when you compare the z-score of the sample mean to the critical value, the critical value comes from z_alpha instead of z_alpha/2.

The same logic applies to the p-value approach.

Lecture 6 - Ch 9 - Hypothesis Testing

Null and Alternative Hypotheses

Hypothesis testing involves first creating a hypothesis (usually called the "null hypothesis"), H₀, and an alternative hypothesis, H_a (also sometimes denoted H₁) which is the opposite of the null hypothesis.

For example, we may have historical data about the mean of the population, μ. Our null hypothesis may be that the population mean is still μ. In this case, the alternative hypothesis is that the mean is not equal to μ.

The null hypothesis is always one of status quo - that a parameter is equal to a known, historical value. (As we'll see later, the null hypothesis may be that a parameter is equal to or less than or equal to or greater than a value. In any case, there's always an equal sign in the null hypothesis and never in the alternative hypothesis.) Both hypotheses are always stated about a population parameter, not a sample statistic.

Confidence Level

After stating the null and alternate hypotheses to be tested, our next step is to determine the confidence level of the hypothesis test. This is usually 90, 95 or 99%, depending on how certain we want to be about our rejection or non-rejection of the null hypothesis. In order to determine the confidence level, we consider the level of significance, alpha. The level of significance, alpha, is the probability that we will reject the null hypothesis even though it is true. Not good! This is known as a Type I error and we typically want to minimize it to 0.10, 0.05, or 0.01. The complement of the level of significance is the confidence coefficient, 1-alpha, usually 0.90, 0.95 or 0.99, and represents the probability that we will not reject the null hypothesis when it is true. That would be good! The confidence level is the confidence coefficient stated as a percentage - 90%, 95% or 99%.

In order to decide whether to accept or reject the null hypothesis, we take a sample and calculate its mean. Then we construct a confidence interval around the population mean with the given confidence level. If the sample mean falls within the confidence interval, we do not reject the null hypothesis. If the sample mean falls outside the confidence interval, we reject the null hypothesis in favor of the alternative hypothesis.

Critical Value Method

Example:
H₀: population mean (mu) = 160
H_a: mu does not equal 160
level of significance = 0.10
confidence coefficient = 0.90
confidence level = 90%
sample size (n) = 36
sample mean (xbar) = 172
population std dev (sigma) = 30

Rather than go through all the calculations of constructing the confidence interval, we can just look at the z value of the sample mean compared to the z value of the confidence interval. This is known as getting the critical value. Big note: This only works if you know the population standard deviation! If you don't, you'll need to use the t-distribution and get the t-value using the sample std dev.

For the 90% confidence interval: z_0.05 = -1.65
For the sample mean: z = (160-172)/(30/sqrt(36)) = -12/5 = -2.4

The important part to remember here is that the z-score that we calculate is z_alpha/2. We use alpha/2 because the rejection region is divided into two halves on either side of the distribution. I.e. we would reject the null hypothesis is our sample mean was too high or too low.

In this case, the non-rejection region is from -1.65 to +1.65. Since the z score of the sample mean is outside the non-rejection region of the 90% interval (it's less than -1.65), we say that the sample leads us to reject the null hypothesis.

Example 2:
same as example 1 except - sample mean (xbar) = 165

In this case, the z score of the sample mean is (160-165)/(30/sqrt(36)) = -5/5 = -1

Since the z score of the sample mean is within the non-rejection region of the 90% interval (i.e. it's between -1.65 and +1.65), we say that we cannot reject the null hypothesis. It doesn't really tell us that we should accept the null hypothesis, but we don't have sufficient evidence to reject it.

p-value Method
Another equivalent way of evaluating the null hypothesis is the p-value method. The p-value is the area under the normal distribution curve over a given value.

For example 2 above, we find that from the normal distribution table the area under the curve from the mean to 1.0 (the z-score of the sample mean) is 0.34. Therefore, the p-value of the sample mean (1.0) is 0.5-0.34 = 0.16

We compare this value to the area under the curve above our confidence interval, which is alpha/2 = 0.05. Since the p-value of the sample value is greater then alpha/2, we do not reject the null hypothesis, H₀. If we find that the p-value of the sample mean is less than alpha/2, we would reject H₀.

As our book says: If the p-value is low, H₀ must go!

It seems that the advantage of using the p-value method is that it only requires one lookup into the normal distribution table, whereas the critical value method requires two lookups.

Lecture 6 - Ch 8c - Determining Sample Size

Determining Sample Size

Up until now in this chapter, we've determined the confidence interval based on a give sample. We now ask how to determine the appropriate sample size based on a known confidence level. We ask ourselves - if we want to know the mean within a certain margin of error with a xx% confidence, how large a sample do we need to take?

Margin of Error (e) = z_alpha/2(sigma/sqrt(n))

When we know the desired margin of error ahead of time, we call it the "maximum tolerable error".

Solving the equation above for n, we get:
n = (z_alpha/2sigma/e)²

Example:
What sample size should we use if we want a 90% confidence interval with a maximum tolerable error of +/- 5 with a population that has std dev of 45?

Answer:
z_alpha/2 for 90% (alpha=0.1) is 1.645.
So, n = ((1.645)(45)/5)² = 219.19
Therefore use a sample size of 220.

Lecture 6 - Ch 8b - Confidence Interval for the Mean with *Unknown* Std Dev - Examples and Minitab

Example Problems
We did the following example problems (I'm not sure I captured all the details of the problems, but I think I got the important parts):

Ex1: Sample size, n=17
Find a 95% confidence interval.
A1: 0.95 is 1-alpha, so your alpha is 0.05. Therefore, you want to look up t_0.025,16, which is 2.120

Ex2: Sample size, n=14
Find a 90% confidence interval.
A2: 0.90 is 1-alpha, so your alpha is 0.1. Therefore you look up t_0.05,13, which is 1.771

Ex3: Sample size, n=25. xbar=50, s=8
Find a 95% confidence interval for the mean.
A3: From the t-table, you find t_0.025,24 is 2.064
Therefore, the 95% confidence interval for the mean is 50 +/- 2.064 (8/sqrt(25))

Ex4: (This is problem 8.69 in the book) Sample size, n=50, xbar=5.5, s=0.1
Find a 99% confidence interval for the mean.
A4: 0.99 is 1-alpha, so alpha is 0.01. We look up t_0.005,49 which is 2.68. (If your table doesn't list degrees of freedom for the one you're looking for, just use the closest one. In our case, I think we used 50 instead of 49. Close enough!)
Therefore, the 99% confidence interval for the mean is 5.5 +/- 2.68(0.1/sqrt(50))
= 5.5 +/- 0.0379
= (5.4621,5.5379)

Using Minitab to find Confidence Intervals

In Minitab, pull up your data into a column. We used the teabags.mtw sample data from the textbook problem 8.69. Select Stat - Basic Statistics - 1 sample t from the menu bar. Select your data column in the Samples in columns section. Click Options and set your confidence interval.

The output from Minitab looks like this:
Variable N Mean StDev SE Mean 99% CI
Teabags 50 5.50140 0.10583 0.01497 (5.46129, 5.54151)

Unfortunately, it doesn't give us the critical value of t (which we calculated to be 2.68). But you can see that the confidence interval is pretty much the same as the answer we got above manually. I think the difference is due to the fact that Minitab used more precise values for the mean and std dev.

Lecture 6 - Ch 8b - Confidence Interval for the Mean with *Unknown* Std Dev

The Central Limit Theorem tells us that xbar (the mean of a sample) is normally distributed around the population mean with std dev of sigma/sqrt(n).

Equivalently, we can say that the z-score (xbar-mu)/(sigma/sqrt(n)) is normally distributed around 0 with std dev of 1.

In the case where we don't know the standard deviation of the mean, we can only look at the distribution of the variable t = (xbar-mu)/(s/sqrt(n)), where s is the std dev of the sample.

In the early 1900s, a statistician for Guinness Brewery (now that's a job I'd like to have!) developed a formula for the t distribution as a function of n. Actually, it's usually expressed as a function of (n-1) which is called the "degrees of freedom" in the sample.

The actual function for t is incredibly complex. It looks like this:
Please, do not try to remember that!

What you do need to know is that just like the binomial, poisson and normal distributions, math majors seeking something productive to do have spent countless hours calculating the values for the t-distribution and putting them in tables.

The way the t-table works is almost the opposite of the way the normal distribution table works. The normal distribution table assumes you know a z-score and the table tells you the area under the curve corresponding to that z-score (either from the mean to the z-score in table e.11 or from -infinity to the z-score in table e.2).

The t-distribution table assumes you know the area under the curve and the degrees of freedom (n-1) and the table tells you the corresponding "t-score", which is called the Critical Value.

The shape of the t-distribution is similar to the normal distribution except that it has fatter tails at low values of n. As n gets larger, the t-distribution is almost identical to the normal distribution. In class, we said that they are essentially identical for n>=30. In the book, it gives a value of 120 for n for the two distributions to be considered identical.

To graphically demonstrate how the t-distribution converges on the normal distribution as n increases, we watched an online java applet demonstration that allows us to manually vary n and watch how the two distributions become more and more similar as n increases.