Lecture 8 - Residual Analysis - Checking Linearity

Checking Linearity
Our method for checking the first assumption, linearity of the data, is not a precise, quantitative test. Rather, we'll use visual inspection to check for linearity.

One quick way to test the linearity of the data is to create an x-y scatter plot and observe whether the data generally follows a straight line (either with positive or negative slope). Plotting the regression line through the data may help visualize this as well.

Using Minitab for the linearity check:
1. Bring up your data in a worksheet. We used the site.mtw file in class.
2. Select Graph-Scatterplot from the menu bar. Select the "With Regression" option when prompted for the type of scatterplot.
3. Put Annual Sales (the dependent variable) in the Y Variables column and Square Feet (the independent variable) in the X Variables column. Remember that the independent variable is the variable that you can control and which you think will be a predictor of the dependent variable. In other words, the annual sales is dependent on the size of the store (in square feet). It's not the other way around. The size of the store doesn't grow or shrink depending on the number of sales!
4. Don't change the default options and click OK. You should get a plot of your data with a regression line through it. (If you don't get the regression line, in step 3 click Data View, Regression Tab and make sure Linear is selected.)

To interpret the linearity of this graph, "eyeball" the way the points fall above and below the regression line and ask yourself: Are the data points relatively linear or is it curved or skewed in some way? In our case, the data is relatively linear and not curved, so we conclude that the assumption of linearity is valid.

A better way to visually assess the linearity is to plot the residuals versus the independent variable and look to see if the errors are distributed evenly above and below 0 along the entire length of the sample.

Plotting Residuals versus the Independent Variable with Minitab
1. Select Stat-Regression from the menu bar.
2. Put Annual Sales in the Response box and Square Feet in the Predictors box. In our scenario, we think that the number of square feet will be a predictor of the annual sales of the store. Notice that the predictors box is large. There can be more than one predictor - perhaps advertising, employee training, etc. Many things can influence the response variable - the annual sales. We'll get to that during multiple linear regression. Right now, for simple linear regression, we're just looking at a single predictor.
3. Click the Graphs button. Put Square Feet in the Residuals versus the variables box.

To interpret this graph, ask yourself: Do the residual points fall equally above and below 0 along the entire length of the horizontal axis? In our case, the residuals do more or less fall equally above and below 0, so we conclude that the data is linear and the assumption of linearity is valid. Note: We also see that the residuals are closer to 0 for lower values of x (square feet). That may become important later when we talk about equal variance of errors.

Lecture 8 - Residual Analysis - Definition

Residual Analysis
In Lecture 7 we discussed how to use the method of least-square to perform simple linear regression on a set of data. We also discussed the four assumptions we make about our data in order to use the method of least-squares for the regression:
1. Linearity
2. Independence of errors
3. Normality of error
4. Equal variance of errors

The error is also known as the residual and is the difference between the observed Y_i value, for any particular X_i, and the value for Y_i predicted by our regression model which is usually symbolized by Ŷ_i (read "y hat sub i"). The residual is symbolized by the greek letter epsilon (lower case) - ε_i.

ε_i = Y_i - Ŷ_i

We perform a four-part residual analysis on our data to evaluate whether each of the four assumptions hold and, based on the outcome, we can determine whether our linear regression model is the correct model.

It's called a residual analysis because 3 of the 4 assumptions (independence, normality and equality of variance) directly relate to the errors (the residuals) and the other assumption (linearity) is tested by assessing the residuals.

Using the DePaul Online Library for Research

DePaul Online Research Library
One of the really nice perks that we have as students at DePaul is the online research library. The library subscribes to many databases of academic journals and magazines which are searchable. Many of these databases allow you to access and download full text versions of the journal articles, usually available in PDF format. To access the online research library, all you need is your Depaul student ID.

Another really nice feature of the DePaul online research library is that it can be integrated with the Google Scholar search engine. I'll show you how to do that in a future blog post.

Here's how to access the DePaul online research library:
1. Bring up the main DePaul web site by browsing to http://www.depaul.edu.
2. At the top of the page, click on the "Libraries" link.

3. This will bring you to the Library page. There are lots of links to follow here. Focus on the "Research" section. The way this works is that you need to identify the database in which you want to conduct your search. Once you do that, you can use the database's internal search function to find your article. So, how do you find a database? There are a couple ways:

Method 1:
Use this method if you're just starting out and don't know which database or journal you're going to search
4. Click the "Journals and newspaper articles" link. That will bring you to the subject page.
5. Since we're studying statistics, a good choice for subject would be Mathematical Sciences. Click that link.
6. You get the database list. For mathematical sciences, we subscribe to 7 databases. The database list gives you a short description of the database and the dates covered by the database. Some of the databases indicate whether we subscribe to full text of articles with a FT icon:

7. Choose your database and click on its link. You'll be prompted for your DePaul username and password. Enter those and click Login.

Method 2:
Use this method if you know the database you want to search
4. In the Research section of the Library page you can click on the A-Z Database List to see all the databases. If you already know the database that you want to search, you can skip by the "subject" steps 4-5 above in method 1 by just using the A-Z list.

Method 3:
Use this method if you know the name of the journal that you want to search
4. Click the "Journals and newspaper articles" link.
5. On the left hand margin, enter the name of the journal and click Search.
6. The results page will show you which databases contain that journal and for which years

Each database has its own interface and it would be impossible for me to cover all of them, but most of them are self explanatory and user-friendly. You can usually search by author, article title or keyword. Several databases also allow you to browse the issues of the journals in the database.

More to come...

Lecture 7 - Coefficient of Determination

After calculating β₀ and β₁ to determine the best line to fit the data, we want to quantify how well the line fits the data. It may be the best line, but how good is it?

Sum of Squares
Looking at the graph of the data, we could say that without any modeling or regression at all, we would expect the y-value for any give x to be the mean y, ybar. Most of the observations, of course, would not be equal to the mean. We can measure how far the observations are from the mean by taking the difference between each y_i and ybar, squaring them, and taking the sum of the squares. We call this the total sum of squares or SST.

You probably remember that the variance that we discussed much earlier in the course is this sum of squares divided by n-1.

The total sum of squares is made up of two parts - the part that is explained by the regression (yhat-ybar) and the part that the observation differs from the regression (y_i-yhat). When we square each of these and sum them we compute the regression sum of squares, SSR, and the error sum of squares, SSE.

Coefficient of Determination
The 3 sum of squares terms, SST, SSR and SSE, don't tell us much by themselves. If we're dealing with observations which use large units, these terms may be relatively large even though the variance from a linear relationship is small. On the other hand, if the units of the measurements in our observations is small, the sum of square terms may be small even when the variance from linearity is great.

Therefore, the objective statistic that we use to assess how well the regression fits the data is the ratio of the regression sum of squares, SSR, to the total sum of squares, SST. We call this statistic the coefficient of determination, r².

r² = SSR / SST

Lecture 7 - Assumptions in the Method of Least Squares

Photo courtesy of F. Espenak at MrEclipse.com

Assumptions
In order to use the Least Squares Method, we must make 4 fundamental assumptions about our data and the underlying relationship between the independent and dependent variables, x and y.

1. Linearity - that the variables are truly related to each other in a linear relationship.
2. Independence - that the errors in the observations are independent from one another.
3. Normality - that the errors in the observations are distributed normally at each x-value. A larger error is less likely than a smaller error and the distribution of errors at any x follows the normal distribution.
4. Equal variance - that the distribution of errors at each x (which is normal as in #3 above) has the identical variance. Errors are not more widely distributed at different x-values.

A useful mnemonic device for remembering these assumptions is the word LINE - Linearity, Independence, Normality, Equal variance.

Note that the first assumption, linearity, refers to the true relationship between the variables. The other three assumptions refer to the nature of the errors in the observed values for the dependent variable.

If these assumptions are not true, we need to use a different method to perform the linear regression.

The Least-Squares Method

The Method of Least Squares
As described in the previous post, the least-squares method minimizes the sum of the squares of the error between the y-values estimated by the model and the observed y-values.

In mathematical terms, we need to minimize the following:
∑ (y_i - (β₀+β₁x_i))

All the y_i and x_i are known and constant, so this can be looked at as a function of β₀ and β₁. We need to find the β₀ and β₁ that minimize the total sum.

From calculus we remember that to minimize a function, we take the derivative of the function, set it to zero and solve. Since this is a function of two variables, we take two derivatives - the partial derivative with respect to β₀ and the partial derivative with respect to β₁.

Don't worry! We won't need to do any of this in practice - it's all been done years ago and the generalized solutions are well know.

To find b₀ and b₁:
1. Calculate xbar and ybar, the mean values for x and y.
2. Calculate the difference between each x and xbar. Call it xdiff.
3. Calculate the difference between each y and ybar. Call it ydiff.
4. b1 = [∑(xdiff)(ydiff)] / ∑(xdiff²)
5. b₀ = ybar - b₁xbar

Notice that we switched from using β to using b? That's because β is used for the regression coefficients of the actual linear relationship. b is used to represent our estimate of the coefficients determined by the least squares method. We may or may not be correctly estimating β with our b. We can only hope!

Lecture 7 - Simple Linear Regression

Linear Regression essentially means creating a linear model that describes the relationship between two variables.

Our type of linear regression is often referred to as simple linear regression. The simple part of the linear regression refers to the fact that we don't consider other factors in the relationship - just the two variables. When we model how several variables may determine another variable, it's called multiple regression - the topic for a more advanced course (or chapter 13 in our text).

For example, we may think that the total sales at various stores is proportional to the number of square feet of space in the store. If we collect data from a number of stores and plot them in an XY scatter plot, we would probably find that the data points don't lie on a perfectly straight line. However, they may be "more or less" linear to the naked eye. Linear regression involves finding a single line that approximates the relationship. With this line, we can estimate the expected sales at a new store, given the number of square feet it will have.

In mathematical terms, linear regression means finding values for β₀ and β₁ in the equation

y = β₀ + β₁x

such that the resulting equation fits the data points as closely as possible.

The equation above may look more familiar to you in this form:

y = mx + b

That's the form we learned in linear algebra. m is the slope and b is the y-intercept. Similarly, in our statistical form, β₁ is the slope and β₀ is the y-intercept.

How Close is Close?
We said that we want to find a line that fits the data "as closely as possible". How close is that? Well, for any given β₀ and β₁, we can calculate how for off we are by looking at each x-value, calculating what the linear estimate would be according to our regression equation and comparing that to the actual observed y-value. The difference is error between our regression estimate and the observation. Clearly, we want to find the line that minimizes the total error.

Minimizing the total error is done in practice by minimizing the sum of the squares of the errors. If we used the actual error term, and not the square, positive and negative errors would cancel each other out. We don't use the absolute value of the error term because we will need to integrate it and the absolute value function is not integrable at 0.

Generating regression coefficients β₀ and β₁ for the linear model by minimizing the sum of the square of the errors is known as the least-squares method.

Homework

In case you were wondering...
According to an email I got from Prof Selcuk, there is no homework due this week. Homework #5 will be assigned this Thursday Feb 28 and due next Thursday March 6. It will be the last homework of the quarter.

My comment: This will give us time to absorb the material on linear regression before working on homework exercises. Maybe even time to go to the zoo on Sunday instead of doing homework.

Lecture 7 - Using Minitab to Calculate Hypothesis Testing Statistics

Using Minitab to Calculate Hypothesis Testing Statistics
Minitab can be used to perform some of the calculations that are required in steps 4 and 5 of the critical value approach and step 4 of the p-value approach to hypothesis testing (see previous 2 posts). You still need to do all the study design in steps 1-3 and use them as input to Minitab. You will also need to draw your own conclusions from the calculations that Minitab performs.

Here's how:
1. Load up your data in a Minitab worksheet. (In lecture 7, we used the data in the insurance.mtw worksheet from exercise 9.59.)
2. Select Stat - Basic Statistics from the menu bar. Since we're doing hypothesis testing of the mean, we have 2 choices from the menu. Either "1-sample z" or "1-sample t". Since we don't know the standard deviation of the population, we choose the "1-sample t" test.
3. In the dialog box, select the column that has your sample data and click the select button so it appears in the "Samples in columns" box. In the test mean box, enter the historical value for the mean, which in our case is 45.
4. Click the Options button and enter the confidence level ((1-&alpha)x100) and select a testing "alternative". The testing alternative is where you specify the testing condition of the alternative hypothesis.

• If H₁ states that the mean is not equal to the historical value, select not equal. Minitab will make calculations for a two-tail test.
• If H₁ states that the mean is strictly less than or strictly greater than the historical value, select less than or greater than. In this case, Minitab will calculate values for a one-tail test.

5. Click Ok in the Options dialog and Ok in the main dialog. Minitab displays the calculated values in the Session window. The results from our sample data looked like this:

One-Sample T: Time
Test of mu = 45 vs not = 45

Variable N  Mean    StDev  SE Mean       95% CI        T    P
Time     27 43.8889 25.2835 4.8658 (33.8871, 53.8907) -0.23 0.821

Unfortunately, Minitab doesn't take the hypothesis testing all the way to drawing a conclusion about the null hypothesis. We need to do that ourselves in one of two ways: either the critical value or p-value approach.

For the critical value approach, we need to additionally look up the t-score for t_0.025,26 = ±2.056. 0.025 is α/2, which we use with this two-tail test. 26 is n-1, the degrees of freedom for this test. We compare t_0.025,26 to the t-score of the sample mean, which Minitab calculated for us as -0.23, and find that the t-score of the sample mean is between the critical values and therefore we do not reject H₀.

For the p-value approach, we compare the p-value that Minitab calculated as 0.821 and compare that to the level of significance, &alpha, which in our case is 0.10. Since the p-value is larger than α we do not reject H₀.

Hypothesis Testing - p-Value Approach - 5 Step Methodology

The p-Value Approach
The p-value approach to hypothesis testing is very similar to the critical value approach (see previous post). Rather than deciding whether or not to reject the null hypothesis based on whether the test statistic falls in a rejection region or not, the p-value approach allows us to make the decision based on whether or not the p-value of the sample data is more or less than the level of confidence.

The p-value is the probability of getting a test statistic equal to or more extreme than the sample result. If the p-value is greater than the level of confidence then we can say that the probability of a more extreme test statistic is larger than the level of confidence and thus we do not reject H₀.

If, on the other hand, the p-value is less than the level of confidence, we conclude that the probability of a more extreme test statistic is smaller than the level of confidence and thus we reject H₀.

The five step methodology of the p-value approach to hypothesis testing is as follows:
(Note: The first three steps are identical to the critical value approach described in the previous post. However, step 4, the calculation of the critical value, is omitted in this method. Differences in the final two steps between the critical value approach and the p-value approach are emphasized.)

State the Hypotheses
1. State the null hypothesis, H₀, and the alternative hypothesis, H₁.
Design the Study
2. Choose the level of significance, α according to the importance of the risk or committing Type I errors. Determine the sample size, n, based on the resources available to collect the data.
3. Determine the test statistic and sampling distribution. When the hypotheses involve the population mean, μ, the test statistic is z when σ is known and t when σ is not known. These test statistics follow the normal distribution and the t-distribution respectively.
Conduct the Study
4. Collect the data and compute the test statistic and the p-value.
Draw Conclusions
5. Evaluate the p-value and determine whether or not to reject the null hypothesis. Summarize the results and state a managerial conclusion in the context of the problem.

Example (we'll look at the same example as the last post, also reviewed at the beginning of Lecture 7):
A phone industry manager thinks that customer monthly cell phone bills have increased and now average over $52 per month. The company asks you to test this claim. The population standard deviation, σ, is known to be equal to 10 from historical data.

The Hypotheses
1.H₀: μ ≤ 52
H₁: μ > 52
Study Design
2. After consulting with the manager and discussing error risk, we choose a level of significance, α, of 0.10. Our resources allow us to sample 64 sample cell phone bills.
3. Since our hypothesis involves the population mean and we know the population standard deviation, our test statistic is z and follows the normal distribution.
The Study
4. We conduct our study and find that the mean of the 64 sample cell phone bills is 53.1. We compute the test statstic, z = (xbar-μ)/(σ/√n) = (53.1-52)/(10/√64) = 0.88. Next, we look up the p-value of 0.88. The cumulative normal distribution table tells us that the area to the left of 0.88 is 0.8106. Therefore, the p-value of 0.88 = 1-0.8106 = 0.1894.
Conclusions
5. Since 0.1894 is greater than the level of significance, α, we do not reject the null hypothesis. We report to the company that, based on our testing, there is not evidence that the mean cell phone bill has increased from $52 per month.

Hypothesis Testing - Critical Value Approach - 6 Step Methodology

The six-step methodology of the Critical Value Approach to hypothesis testing is as follows:
(Note: The methodology below works equally well for both one-tail and two-tail hypothesis testing.)

State the Hypotheses
1. State the null hypothesis, H₀, and the alternative hypothesis, H₁.
Design the Study
2. Choose the level of significance, α according to the importance of the risk or committing Type I errors. Determine the sample size, n, based on the resources available to collect the data.
3. Determine the test statistic and sampling distribution. When the hypotheses involve the population mean, μ, the test statistic is z when σ is known and t when σ is not known. These test statistics follow the normal distribution and the t-distribution respectively.
4. Determine the critical values that divide the rejection and non-rejection regions.
Note: For ethical reasons, the level of significance and critical values should be determined prior to conducting the test. The test should be designed so that the predetermined values do not influence the test results.
Conduct the Study
5. Collect the data and compute the test statistic.
Draw Conclusions
6. Evaluate the test statistic and determine whether or not to reject the null hypothesis. Summarize the results and state a managerial conclusion in the context of the problem.

Example (reviewed at the beginning of Lecture 7):
A phone industry manager thinks that customer monthly cell phone bills have increased and now average over $52 per month. The company asks you to test this claim. The population standard deviation, σ, is known to be equal to 10 from historical data.

The Hypotheses
1.H₀: μ ≤ 52
H₁: μ > 52
Study Design
2. After consulting with the manager and discussing error risk, we choose a level of significance, α, of 0.10. Our resources allow us to sample 64 sample cell phone bills.
3. Since our hypothesis involves the population mean and we know the population standard deviation, our test statistic is z and follows the normal distribution.
4. In determining the critical value, we first recognize this test as a one-tail test since the null hypothesis involves an inequality, ≤. Therefore the rejection region is entirely on the side of the distribution greater than the historic mean - right tail.
We want to determine a z-value for which the area to the right of that value is 0.10, our α. We can use the cumulative normal distribution table (which gives areas to the left of the z-value) and find z having value 0.90 = 1.285. This is our critical value.
The Study
5. We conduct our study and find that the mean of the 64 sample cell phone bills is 53.1. We compute the test statstic, z = (xbar-μ)/(σ/√n) = (53.1-52)/(10/√64) = 0.88.
Conclusions
6. Since 0.88 is less than the critical value of 1.285, we do not reject the null hypothesis. We report to the company that, based on our testing, there is not evidence that the mean cell phone bill has increased from $52 per month.

Hypothesis Testing - Definitions

Definitions
In this post I define terms used in the lectures and textbook in the discussion of hypothesis testing.

Hypothesis Testing: a decision-making process for evaluating claims about a population.

Null Hypothesis (H₀): a conjecture that states that a population parameter is equal to a certain value. The value chosen is usually based on historical data or some other reliable source. The null hypothesis may also state that a population parameter is greater than or equal to or less than or equal to a certain value. In any case, the null hypothesis always contains an equality.

Alternative Hypothesis (H₁ or H_A): a conjecture that states that a population parameter is not equal to a certain value. The alternative hypothesis is the complement of the null hypothesis.

Examples:
H₀: μ = 56
H₁: μ ≠: 56

H₀: μ ≤ 4.5
H₁: μ >: 4.5

H₀: μ ≥ $102
H₁: μ <: $102

Note: In these examples, I use the parameter μ, the population mean, because we looked at hypothesis testing of the mean in the lecture. However, there are methods for doing hypothesis testing for the proportion (section 9.5 in our text) as well as other parameters which we did not cover.

Rejection Region: An area of the sampling distribution. If the test statistic falls into the rejection region, we reject the null hypothesis in favor of the alternative hypothesis.

Non-rejection region: An area of the sampling distribution which is the complement of the rejection region. If the test statistic falls in the non-rejection region, we say that we do not have evidence to reject the null hypothesis.

Critical Value: The value which divides the rejection region from the non-rejection region.

Type I Error: An error of rejecting the null hypothesis, H₀, when it is true.
Type II Error: An error of not rejecting the null hypothesis, H₀, when it is false.

Level of Significance, α: The probability of committing a Type I error in a statistical test. Typically, the level of significance is controlled by specifying this value before the test is conducted and determining the rejection region based on it. A lower level of significance (lower probability of Type I error) requires a smaller rejection region because we are more cautious not to reject H₀. Typical values for α are 0.01, 0.05 and 0.10.
Confidence Coefficient: The complement of the level of significance: 1 - α.
Confidence Level: The confidence coefficient expressed as a percentage: (1 - α) x 100.

β (Beta) Risk: The probability of committing a Type II error in a statistical test. The value of the β risk is difficult to determine. Among other factors, it depends on the difference between the hypothesized value of the parameter being tested and the actual value of the parameter. If we knew that difference, we wouldn't need to do any testing!
Power of a Test: The complement of the β risk: 1 - β.

Two-Tail Test: A statistical test in which the null hypothesis, H₀, is that a population parameter is strictly equal to a specific value. In such a case, the rejection region is divided into two halves (i.e. two tails) on either side of the sampling distribution of the test statistic.

One-Tail Test: A statistical test in which the null hypothesis, H₀, is either greater than or equal to or less than or equal to a specific value. In such a case, the rejection region is entirely on one half (i.e. one tail) of the sampling distribution of the test statistic.

Homework #4

It's kind of last minute, but... Exercises for Homework #4, due tomorrow, are:
8.19
8.21 a
8.43
8.65 a and c
9.31
9.45
9.59 a

In bothers me a bit that in the hypothesis testing that we're asked to do in the chapter 9 exercises, the sample means seem to fall either significantly outside the non-rejection region or clearly within the non-rejection region. You would think that these problems would involve more borderline cases where the you couldn't just solve the problem by inspection.

Case in point: One problem has a sample that has a std dev of around 25 and the sample mean is only about 1.5 less than the H₀ mean and we're asked to assess H₀ at a 0.05 level of significance. Isn't it obvious?

Reading the Normal Distribution Tables

There are two different normal distribution tables. In our textbook they're labeled e.2 and e.11. (A third table on the page after the inside front cover of the book is identical to table e.2.)

What's the difference?

The first table (e.2) is the cumulative standard normal distribution table. With it, you can look up the area under the standard normal distribution function from -∞ to any particular z-score, either positive or negative.

Download a MS Word version of this table.

The second table (e.11) is the plain, old (not cumulative) standard normal distribution table. The values that you look up in that table are the area under the curve from the mean (0 since it's standardized) to your z-score.

You can really use either table in almost any scenario. I typically find the cumulative table easier to work with.

If A_c is the value in the cumulative table (e.2) and A_n is the value in the plain, old table (e.11), the relationship between the two tables is:

for z<0: A_c = 0.5 - A_n (using -z when looking up the value in e.11)

for z>0: A_c = A_n + 0.5

Reading Values from the Table
To use either standard normal distribution table, you first must calculate the z-score(s) that are of interest. The z-score is the number of standard deviations from the mean for your target value, X.

For example, if you have a normal distribution with mean 20 and standard deviation 3 and you want to know the probability of an observation being less than 22, you calculate the z-score as:

z = (X-μ)/σ = (22-20)/3 = 0.67

Our z-score tells us that we want to know the probability of an observation being less than 0.667 standard deviations from the mean. We turn to the cumulative standard normal distribution table to find this probability.

We go down the first column until we get one decimal point of accuracy (0.6) and then we move across the table to the row which gives us the second decimal point of accuracy (0.07). The value at the intersection is our answer!

So P(X<22) = 0.7486 = 74.86%

Exit Polls

Having gone over the concept of sample size, it's interesting to turn to one of the most well-known samplings: election exit polls. Who does these exit polls and how are they performed?

As it turns out, ABC, Associated Press, CBS, CNN, Fox and NBC formed a consortium in 2003 called the National Election Pool (NEP). NEP then contracted with Edison/Mitofsky to conduct exit polls across the country and provide analysis and projections.

According to the latest news on the Edison/Mitofsky site, they sampled 2300 voters (1442 democrats and 880 republicans) in yesterday's Wisconsin primary. You can find the details of all the Wisconsin exit poll questions at CNN's web site.

The Milwaukee Journal Sentinal reports the details of the actual vote count broken down by county and congressional district for both the Democratic and Republican primaries. The total number of reported voters is about 1,515,630 (1,108,119 democrats and 407,511 republican) .

On the democratic side, the exit polls showed Obama had 57.1% of the votes and Clinton had 42.0%. In the final tally, Obama beat Clinton 58% to 41%. It turns out that the exit polls were accurate within about 1% or 15,000 votes.

Graphing the Normal Distribution Curve with Excel

I know... You're thinking to yourself: How does he make such awesome normal distribution curves for those illustrations on this blog? He can't be drawing them by hand! Well, I learned the basics from Gary Andrus's web page, and then I modified his method to make it more general and a bit faster.

Here's how I do it using MS Excel 2003 (and I'll even throw in a few nice Excel tricks too):

Step 1: In cell A1 enter -4. In cell A2 enter -3.75. Now, highlight both cells and grab that little box in the lower right hand corner of A2 that turns into a plus sign when you hover your mouse over it (it's called the "fill handle") and drag it down to cell A33. Release your mouse and (wolla!) your first column is filled with numbers from -4 to 4 in increments of 0.25.

Step 2: In cell B1 enter =NORMDIST(A1,0,1,0). This tells Excel to calculate the value of the normal distribution PDF for the value in A1 (which is -4) for a normal distribution with mean of 0 and standard deviation 1. I.e. the standard normal distribution. You can fiddle with those values if you want a different normal distribution. The last 0 tells it to use the probability distribution function, not the cumulative distribution function (you overachievers can try using 1 as your last value for extra credit).

Now, you could use the same handy-dandy trick with the "fill handle" that I showed you in step 1 to propagate the NORMDIST function down column B. But I'll show you another way just for kicks. Highlight cells B1 through B33 and hit Ctrl+D. It fills the values down the column. (Think "D" for "down". Ctrl+R works the same way when you select cells to the right. But Ctrl+L and Ctrl+U don't.)

Step 3: Select all your data points - the region A1 through B33 and hit the Chart Wizard button on the toolbar (or Insert-Chart on the menu bar). In the Chart Wizard step 1, select the XY Scatter chart type and the smooth lines without markers sub-type. Click Next. Click Next for step 2 without changing anything. In step 3, on the Axes tab unselect the y axis, in the Gridlines tab unselect the y axis major gridlines, and in the Legend tab unselect Show legend. Click Next. Click Finish in step 4. Ta-da! Your normal distribution curve magically appears before your very eyes.

Step 4: I usually make it look a little bit nice by right-clicking the x-axis, selecting Format Axis, and in the Scale tab changing the Minimum and Maximum to -4 and 4 respectively. I also right-click the graph line itself, select Format Data Series, and in the Patterns tab I give the line a heavier Weight than the default so it stands out better.

After you're done, you can copy and paste your graph into MS Paint, Paint.NET, Paint Shop Pro or any other graphics program you have to fill it in with colors and/or add explanatory text.

Lecture 6 - Ch 9b - One-Tail Hypothesis Testing

When the null hypothesis is that the current population mean equals the historic mean and the alternative hypothesis is that it does not equal the historic mean, we construct a two-tailed rejection region on either side of the distribution. We reject H₀ is the sample mean is too high to too low.

However, that's not always the case. Sometimes, our null hypothesis is that the mean is at least equal to the historic mean (but possibly larger). In such a case, we would only reject H₀ if it was less than the lower bound (critical value) of the non-rejection region.




Similarly, sometimes our H₀ is that the mean is at most equal to the historic mean (but possibly smaller). In this a case, we would only reject H₀ if it was greater than the lower bound (critical value) of the non-rejection region.

The methodology for doing a one-tail hypothesis test is almost the same as for the two-tail test. The major difference is that our entire rejection region is on one side of the distribution. Therefore, when you set the level of significance, alpha, and the confidence level, (1-alpha)x100, that reflects only one side of the distribution.

Practically speaking, it means that when you compare the z-score of the sample mean to the critical value, the critical value comes from z_alpha instead of z_alpha/2.

The same logic applies to the p-value approach.

Lecture 6 - Ch 9 - Hypothesis Testing

Null and Alternative Hypotheses

Hypothesis testing involves first creating a hypothesis (usually called the "null hypothesis"), H₀, and an alternative hypothesis, H_a (also sometimes denoted H₁) which is the opposite of the null hypothesis.

For example, we may have historical data about the mean of the population, μ. Our null hypothesis may be that the population mean is still μ. In this case, the alternative hypothesis is that the mean is not equal to μ.

The null hypothesis is always one of status quo - that a parameter is equal to a known, historical value. (As we'll see later, the null hypothesis may be that a parameter is equal to or less than or equal to or greater than a value. In any case, there's always an equal sign in the null hypothesis and never in the alternative hypothesis.) Both hypotheses are always stated about a population parameter, not a sample statistic.

Confidence Level

After stating the null and alternate hypotheses to be tested, our next step is to determine the confidence level of the hypothesis test. This is usually 90, 95 or 99%, depending on how certain we want to be about our rejection or non-rejection of the null hypothesis. In order to determine the confidence level, we consider the level of significance, alpha. The level of significance, alpha, is the probability that we will reject the null hypothesis even though it is true. Not good! This is known as a Type I error and we typically want to minimize it to 0.10, 0.05, or 0.01. The complement of the level of significance is the confidence coefficient, 1-alpha, usually 0.90, 0.95 or 0.99, and represents the probability that we will not reject the null hypothesis when it is true. That would be good! The confidence level is the confidence coefficient stated as a percentage - 90%, 95% or 99%.

In order to decide whether to accept or reject the null hypothesis, we take a sample and calculate its mean. Then we construct a confidence interval around the population mean with the given confidence level. If the sample mean falls within the confidence interval, we do not reject the null hypothesis. If the sample mean falls outside the confidence interval, we reject the null hypothesis in favor of the alternative hypothesis.

Critical Value Method

Example:
H₀: population mean (mu) = 160
H_a: mu does not equal 160
level of significance = 0.10
confidence coefficient = 0.90
confidence level = 90%
sample size (n) = 36
sample mean (xbar) = 172
population std dev (sigma) = 30

Rather than go through all the calculations of constructing the confidence interval, we can just look at the z value of the sample mean compared to the z value of the confidence interval. This is known as getting the critical value. Big note: This only works if you know the population standard deviation! If you don't, you'll need to use the t-distribution and get the t-value using the sample std dev.

For the 90% confidence interval: z_0.05 = -1.65
For the sample mean: z = (160-172)/(30/sqrt(36)) = -12/5 = -2.4

The important part to remember here is that the z-score that we calculate is z_alpha/2. We use alpha/2 because the rejection region is divided into two halves on either side of the distribution. I.e. we would reject the null hypothesis is our sample mean was too high or too low.

In this case, the non-rejection region is from -1.65 to +1.65. Since the z score of the sample mean is outside the non-rejection region of the 90% interval (it's less than -1.65), we say that the sample leads us to reject the null hypothesis.

Example 2:
same as example 1 except - sample mean (xbar) = 165

In this case, the z score of the sample mean is (160-165)/(30/sqrt(36)) = -5/5 = -1

Since the z score of the sample mean is within the non-rejection region of the 90% interval (i.e. it's between -1.65 and +1.65), we say that we cannot reject the null hypothesis. It doesn't really tell us that we should accept the null hypothesis, but we don't have sufficient evidence to reject it.

p-value Method
Another equivalent way of evaluating the null hypothesis is the p-value method. The p-value is the area under the normal distribution curve over a given value.

For example 2 above, we find that from the normal distribution table the area under the curve from the mean to 1.0 (the z-score of the sample mean) is 0.34. Therefore, the p-value of the sample mean (1.0) is 0.5-0.34 = 0.16

We compare this value to the area under the curve above our confidence interval, which is alpha/2 = 0.05. Since the p-value of the sample value is greater then alpha/2, we do not reject the null hypothesis, H₀. If we find that the p-value of the sample mean is less than alpha/2, we would reject H₀.

As our book says: If the p-value is low, H₀ must go!

It seems that the advantage of using the p-value method is that it only requires one lookup into the normal distribution table, whereas the critical value method requires two lookups.

Lecture 6 - Ch 8c - Determining Sample Size

Determining Sample Size

Up until now in this chapter, we've determined the confidence interval based on a give sample. We now ask how to determine the appropriate sample size based on a known confidence level. We ask ourselves - if we want to know the mean within a certain margin of error with a xx% confidence, how large a sample do we need to take?

Margin of Error (e) = z_alpha/2(sigma/sqrt(n))

When we know the desired margin of error ahead of time, we call it the "maximum tolerable error".

Solving the equation above for n, we get:
n = (z_alpha/2sigma/e)²

Example:
What sample size should we use if we want a 90% confidence interval with a maximum tolerable error of +/- 5 with a population that has std dev of 45?

Answer:
z_alpha/2 for 90% (alpha=0.1) is 1.645.
So, n = ((1.645)(45)/5)² = 219.19
Therefore use a sample size of 220.

Lecture 6 - Ch 8b - Confidence Interval for the Mean with *Unknown* Std Dev - Examples and Minitab

Example Problems
We did the following example problems (I'm not sure I captured all the details of the problems, but I think I got the important parts):

Ex1: Sample size, n=17
Find a 95% confidence interval.
A1: 0.95 is 1-alpha, so your alpha is 0.05. Therefore, you want to look up t_0.025,16, which is 2.120

Ex2: Sample size, n=14
Find a 90% confidence interval.
A2: 0.90 is 1-alpha, so your alpha is 0.1. Therefore you look up t_0.05,13, which is 1.771

Ex3: Sample size, n=25. xbar=50, s=8
Find a 95% confidence interval for the mean.
A3: From the t-table, you find t_0.025,24 is 2.064
Therefore, the 95% confidence interval for the mean is 50 +/- 2.064 (8/sqrt(25))

Ex4: (This is problem 8.69 in the book) Sample size, n=50, xbar=5.5, s=0.1
Find a 99% confidence interval for the mean.
A4: 0.99 is 1-alpha, so alpha is 0.01. We look up t_0.005,49 which is 2.68. (If your table doesn't list degrees of freedom for the one you're looking for, just use the closest one. In our case, I think we used 50 instead of 49. Close enough!)
Therefore, the 99% confidence interval for the mean is 5.5 +/- 2.68(0.1/sqrt(50))
= 5.5 +/- 0.0379
= (5.4621,5.5379)

Using Minitab to find Confidence Intervals

In Minitab, pull up your data into a column. We used the teabags.mtw sample data from the textbook problem 8.69. Select Stat - Basic Statistics - 1 sample t from the menu bar. Select your data column in the Samples in columns section. Click Options and set your confidence interval.

The output from Minitab looks like this:
Variable N Mean StDev SE Mean 99% CI
Teabags 50 5.50140 0.10583 0.01497 (5.46129, 5.54151)

Unfortunately, it doesn't give us the critical value of t (which we calculated to be 2.68). But you can see that the confidence interval is pretty much the same as the answer we got above manually. I think the difference is due to the fact that Minitab used more precise values for the mean and std dev.

Lecture 6 - Ch 8b - Confidence Interval for the Mean with *Unknown* Std Dev

The Central Limit Theorem tells us that xbar (the mean of a sample) is normally distributed around the population mean with std dev of sigma/sqrt(n).

Equivalently, we can say that the z-score (xbar-mu)/(sigma/sqrt(n)) is normally distributed around 0 with std dev of 1.

In the case where we don't know the standard deviation of the mean, we can only look at the distribution of the variable t = (xbar-mu)/(s/sqrt(n)), where s is the std dev of the sample.

In the early 1900s, a statistician for Guinness Brewery (now that's a job I'd like to have!) developed a formula for the t distribution as a function of n. Actually, it's usually expressed as a function of (n-1) which is called the "degrees of freedom" in the sample.

The actual function for t is incredibly complex. It looks like this: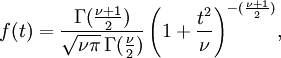
Please, do not try to remember that!

What you do need to know is that just like the binomial, poisson and normal distributions, math majors seeking something productive to do have spent countless hours calculating the values for the t-distribution and putting them in tables.

The way the t-table works is almost the opposite of the way the normal distribution table works. The normal distribution table assumes you know a z-score and the table tells you the area under the curve corresponding to that z-score (either from the mean to the z-score in table e.11 or from -infinity to the z-score in table e.2).

The t-distribution table assumes you know the area under the curve and the degrees of freedom (n-1) and the table tells you the corresponding "t-score", which is called the Critical Value.

The shape of the t-distribution is similar to the normal distribution except that it has fatter tails at low values of n. As n gets larger, the t-distribution is almost identical to the normal distribution. In class, we said that they are essentially identical for n>=30. In the book, it gives a value of 120 for n for the two distributions to be considered identical.

To graphically demonstrate how the t-distribution converges on the normal distribution as n increases, we watched an online java applet demonstration that allows us to manually vary n and watch how the two distributions become more and more similar as n increases.

Lecture 6 - Ch 8b - Confidence Interval for the Mean with *Known* Std Dev

A more realistic example of confidence intervals for the mean would be the case in which the standard deviation of the population is unknown. I mean, how often would you know the standard deviation of the population but not know the mean??

But as a reminder, we did an example where the population std dev is known.

A sample of 11 circuits from a large normal population has a mean resistance of 2.20 ohms. We know from past testing that the population standard deviation is 0.35 ohms. Determine a 95% confidence interval for the true mean resistance of the population.

As in any scenario (what we used to call "story problems"), the key is to pull out the key pieces of information and identify how they should be used. In this case:
n=11
xbar=2.20
sigma(i.e. population std dev)=0.35
and we want a 95% confidence interval

Our confidence interval is xbar +/- z_alpha/2(sigma/sqrt(n))
= 2.20 +/- 1.96(0.35/sqrt(11))
= 2.20 +/- 0.2088

Note 1: Some textbooks leave out the alpha/2 subscript from z. It's really more precise to leave it in there. It will become important when we start looking at one-tail hypothesis testing in Chapter 9.

Note 2: On an exam, the +/- notation is enough. You don't need to actually calculate the endpoints of the interval.

Quiz #4

Q: Suppose the z-score of xbar is 1.34. Calculate the p-value associated with this z-score.

A: The p-value is the area under the curve of the normal distribution above the given value. From the standard normal distribution table we find that from the mean to 1.34, the area is 0.4099. Since we know that the area under the curve above the mean is 0.5,
p-value of 1.34 = 0.5-0.4099 = 0.0901

Current Employment Statistics from the Bureau of Labor Statistics

Every month, usually on the first Friday, the Current Employment Statistics program (CES) at the Bureau of Labor Statistics (BLS) publishes the Employment Situation report. There are a lot of details that go into the collection of the data, calculation of the statistics and creation of this report.

What interested me was the "Technical Note" in the report that related to sampling error. This relates directly to what we learned about confidence intervals in Chapter 8.

First, you need to know how the data is gathered. The BLS uses data from two surveys - the Current Population Survey and the Current Employment Survey. The CPS, also called the household data, is a sample of 60,000 households. The CES, also called the establishment data, is a sampling of the payroll records 160,000 businesses, which constitutes about 1/3 of all the non-farm workers. Those are two honkin' large sample sets! Each is a snapshot in time on the 12th of the month.

The BLS uses these data to calculate the size of the overall labor force and unemployment rate from the household data. The establishment data is used to estimate the number people employed in industry sectors such as construction, manufacturing, retail, education and government. They also calculate the average hourly and weekly wages each month.

The part that's relevant to our class is that this is a case of a estimating a population based on a sample. Therefore, when they say that the unemployment rate is 4.9% is some confidence interval around that number. Here's what the Employment Situation report Technical Note has to say about their sampling error:

When a sample rather than the entire population is surveyed, there is a chance that the sample estimates may differ from the “true” population values they represent. The exact difference, or sampling error, varies depending on the particular sample selected, and this variability is measured by the standard error of the estimate. There is about a 90-percent chance, or level of confidence, that an estimate based on a sample will differ by no more than 1.6 standard errors from the “true” population value because of sampling error.

The 90% confidence interval for the total employment numbers from the household data is +/- 430,000 and for the establishment data it's +/- 104,000. Here are the numbers from the establishment data for total (non-farm) employment in the latest report which includes the data from Nov and Dec 07:

Nov 07 138,037,000
Dec 07 138,119,000
Jan 07 138,102,000

As you can see, all three numbers are within the confidence interval of the statistic, so we can't really say that total employment went up or down in these three months.

You can view the latest report here: The Employment Situation

  I find it hilarious that they use a dinosaur icon for the links to historical data!

Homework #3

In case you didn't get it, the homework problems are:
6.11
6.35 a, b, c, d
7.55 a, b, c, d, e, f
8.7
8.9

Be careful with the parts of 8.7 that ask you to interpret the results of your calculations. Of course, be careful with all the other problems too.

Raw Baseball Data

Thanks to Nathan Yau at FlowingData, I found a link to a site with raw baseball data and stats at Baseball-Databank.org. The files come in csv or mySQL format. If you're not running a mySQL database, the csv files can be easily imported into Excel using the Data-Import External Data menu.

There was an article yesterday by Justin Wolfers on the Freakonomics column/blog at the NY Times which analyzed Roger Clemens's performance against the performance of other pitchers with a long history. The data seemed to indicate that while most pitchers' performance went down over time, Clemens's actually improved during his last few years.

The article has received quite a bit of attention and both Yau and Andrew Gelman have commented on it in their blogs. There has also been feedback from Clemens's PR firm. Interesting reading!

[UPDATE] Justin Wolfers has provided a follow-up article on the Freakonomics blog with a "step-by-step" guide to his analysis. I don't know enough (yet!) about regressions and things like r-squared values to make comments on the analysis, but this seems like a great practical example for us to work through in Chapter 12.

Lecture 5 - Ch 8 - Confidence Interval Estimation

Confidence Interval for a Mean (with known standard deviation)
In previous chapters, we've known the mean value of a normal distribution and, based on the z-table values, said that 90% of the observations will fall +/- 1.65 standard deviations from the mean. Similarly, 95% of the observations will fall +/- 1.96 standard deviations from the mean.

In this chapter, we invert the logic. We say that, given a sample mean, there is a 90% confidence level that the population mean is within +/- 1.65 standard errors of the mean from the sample mean. And similarly, there is a 95% confidence level that the population mean lies withing +/- 1.96 standard errors of the mean from the sample mean.

This type of construction of a confidence interval around a sample mean requires us to know the standard deviation of the population (sigma), from which we calculate the standard error of the mean, sigma/sqrt(n), where n is the sample size. It's not very realistic that we would know the standard deviation of the population and not know its mean. So this is just an exercise. Later in chapter 8, we'll deal with cases where we don't know either the mean or the std dev of the population.

Some terminology
If we want a x% confidence level, we call that 1-alpha.
So if we want a 99% confidence level, 1-alpha = 99% = 0.99. And alpha = 0.01.
Typically, we're looking for a symmetric interval around the sample mean. So in this case we want to know that the population mean falls within 45.5% on either side of the sample mean. Therefore, we look at alpha/2 on each side. We look up z_alpha/2 in the table to find the z-score such that the area in the tail of the curve is alpha/2. Note: this actually means you find the value for 0.5-alpha/2 in the table.

Now we can construct our confidence interval as:
Some common values for Z_alpha/2:
90% confidence interval: Z_0.05 = 1.65
95% confidence interval: Z_0.025 = 1.96
99% confidence interval: Z_0.005 = 2.58

A larger level of confidence requires a larger interval.

I've noted in a prior post that the term "margin of error" seems to be used for the +/- term in the confidence interval in the lecture, but that term is not used at all in the textbook.

Lecture 5 - Ch 7 - Sampling Distributions

This chapter starts us down the road to inferential statistics, i.e. making inferences about the entire population when we only have observations about a sampling or several samplings.

Our first step here is the Central Limit Theorem. The Central Limit Theorem says that if we take many large samples (usually >=30), then

1. the distribution of the sample means is approximately normal
2. the mean of the sample means will be equal to the mean of the population, and
3. the standard deviation of the sample means will be sigma/sqrt(n), where sigma is the standard deviation of the population and n is the sample size.

The Central Limit Theorem holds for any distribution of data.

Therefore, if you don't know anything about the shape of the distribution, but you do know its mean and standard deviation, you can't say much about the probability of individual observations, but you can make inferences about sample sets, such as the mean and standard deviation of the sample set, by assuming (by the CLT) that the distribution of the sample set follows the normal distribution, N(mu,sigma/sqrt(n)).

Here are two videos from Kent Murdick, instructor of mathematics at the University of South Alabama. In the first, he gives a concise, 2 minute overview of the Central Limit Theorem.

In the second video (4 mins), he works through a nice example problem.

Questions for research and thought:
1. What's the proof the Central Limit Theorem? Who discovered it? It's not something that's intuitively obvious at all. See Wolfram's Mathworld which mentions a six-line proof by Kallenberg but does not reproduce it. Their "elementary" proof is considerably longer and involves inverse Fourier transforms. Oh boy!
2. Prof. Murdick added another stipulation in his video - that the sample size, n, must be small (<5%) href="http://en.wikipedia.org/wiki/Central_limit_theorem#_note-nsize">note in the Wikipedia article which references a few scholarly articles that appear to indicate that n>=30 may not be sufficient for the sample size.

Note: We will not be covering section 7.3 - Sampling distribution of the proportion. Sections 7.4 and 7.5 - Types of survey sampling methods and Evaluating survey worthiness - were not mentioned.

Lecture 5 - Ch 6b - Checking for Normality

The cumulative distribution function (CDF) is the function of the area under the probability distribution function from -infinity to x. For the standard normal distribution, the CDF looks like this:
You can use the CDF to check for the normality of a data set, i.e. how closely it fits the normal distribution, by examining how closely the area under the curve of the data fits the CDF. (Question: why compare to the CDF and not the probability distribution function (PDF) itself?) Minitab has two functions that supports checking against the CDF. Both functions are under the Graph menu.

The first is the Empirical CDF option which produces a graph that looks like the graph to the right. The smooth s-shaped line is the normal distribution CDF. The sample dataset (rubber.mtw) is represented by the step-like function which is overlayed on top of it. It apparently fits the normal distribution relatively well. (Note: You can click the graph to enlarge it.)


The second option is the Probability Plot option which adjusts the y-axis so that the CDF function is a straight line rather than s-shaped and can also shows a confidence interval around it. The graph of the same data as above with a 95% confidence interval is shown at right.

The question that remains is how we quantify how well a dataset fits the normal distribution - or any distribution for that matter. I mean, it's nice to eyeball either of the two graphs above and say "yeh, that looks pretty close", but that's not very precise. If the data represented something in which I have a business or financial stake, I would want to know whether the normal distribution model fits the data with more precision.

Lecture 5 - Ch 6b - Standard Normal Distribution

This week we did four things:
1. Reviewed the midterm briefly
2. Completed chapter 6 - normal distribution
3. Chapter 7 - Central Limit Theorem
4. Started chapter 8 - Confidence intervals

Midterm Review
As I suspected, there were questions on short-answer question #3b. You can see my explanation in a previous post. Note that the answer in the answer key posted on Blackboard is slightly incorrect. Rather than 0.117143, the correct answer is 0.1171145.

End of Chapter 6 - Standard Normal Distribution Examples
We pretty much completed chapter 6 in Lecture 4.

The two key steps in dealing with normally distributed data are:
1. Compute the z-score
2. Read the table and process the data.

Computing the z-score of any given x should be simple enough: z = x-mu/sigma, where mu is the mean and sigma is the standard deviation.

Reading the table is also straightforward once you know how to read them. First, calculate the z-score to two decimal places. (If the z-score is negative, ignore the negative sign.) Then find the row for the z-score that you're looking for truncated after the first place after the decimal. Then go across that row to the column for the value of the second decimal of the z-score. I had never worked with these tables before and it wasn't explained in class, so maybe this is obvious to you but it wasn't to me.

Solving single z-score problems
The table gives you the area under the curve from 0 to the z-score. Let's call that value tz. It represents the probablity that a given value is between the mean (o) and z. But that's not always what you want. For a single z-score (call it z), there are 4 possible scenarios for which you might want to know the probability:
1. P(x<z) where z is greater than 0
2. P(x>z) where z is greater than 0
3. P(x<z) where z is less than 0
4. P(x>z) where z is less than 0

1. P(x<z) where z is greater than 0. You want to know the area under the curve to the left of z. I.e. from -infinity to z. Well the green area from 0 to z is the value you just looked up in the table, call it tz. The red area to the left of 0 is 0.5. [Remember that the area under the entire curve is 1 and it's symmetric around 0, so the are to the left and right of 0 are both 0.5.] Therefore, the entire are to the left of z is simply the sum of those two areas. P(x<z) = 0.5 + tz

2. P(x>z) where z is greater than 0. In this case you want to find the area under the curve from z to infinity. I.e. the right hand tail. Since the area from 0 to infinity is 0.5 and the area from 0 to z is tz, you can just subtract the two to get your answer. P(x>z) = 0.5 - tz




3. P(x<z) where z is less than 0. Now we're dealing with z values less than the mean. In this case you want to know the area under the curve to the left of z, i.e. from -infinity to z. You do this similarly to the way you did #2 above. The area from -infinity to 0 is 0.5 and from z to 0 is tz. Subtract the two to get the area under the left hand tail. P(x<z) = 0.5-tz



4. P(x>z) where z is less than 0. Here you need to find the area from z to +infinity. Well, you know the area from z to 0 is tz and the area from 0 out to +infinity is 0.5. So just add them up to get the full area. P(x>z) = 0.5 + tz.




Solving problems with two z-scores
There are 3 possible scenarios where you might be given two values and asked to compute the probability that a given value falls between the two. First, compute the z-scores for each value, z1 and z2.

Now you'll be in one of the following situations:
1. z1 and z2>0
2. z1 and z2<0
3. z1<0 and and z2>0

1. & 2. Both of the first two scenarios can be solved in the same way. Find tz1 and tz2 from the table. Since you're interested in the area under the curve between the two z-scores, just calculate the difference between tz1 and tz2. That's your answer! (If the answer is negative, just ignore the negative sign.) P(z1<x<z2) = tz1-tz2

3. If z1 and z2 are on opposite sides of the mean, you need to find the total area from z1 to 0 and from 0 to z2. All you need to do here is to find tz1 and tz2 from the table and add them up. P(z1<x<z2) = tz1+tz2

I think these seven cases (4 with a single value and 3 with two values) cover just about every case that I've seen in examples. If you can think of an example that these don't cover, let me know.

Note: Make sure you understand how each one of these scenarios works. I find it easiest to draw out a graph (on paper or in my head) of what I'm trying to solve in order to figure out how to solve it. The hardest part of the problems is often figuring out which one of the scenarios you're dealing with and which formula to use. Once you've done that, it's just arithmetic.

Quiz #3

Question:
Calculate the margin of error for a 95% confidence interval where:
the sample size is 64
the sample mean is 350
the population standard deviation is 64

Answer:
The formula for margin of error = x-bar +/- (z-alpha/2)(stddev/sqrt(n))

We find z-alpha/2 for a 95% confidence interval = 1.96 from our class notes. Manually, you work it out as:
alpha = 1-0.95 = 0.05
alpha/2 = 0.05/2 = 0.025
Since the z-scored table gives us the area from 0 to z, we need to use the "complement" of 0.025 which is 0.5-0.025 = 0.475
Do a reverse lookup in a z-score table for 0.475 and we find that it corresponds to a z-score of 1.96.

So,
margin of error = 350 +/- 1.96(64/(sqrt(64)) = 350 +/- (1.96)(8)
= 350 +/- 15.68*

* technically, our textbook refers to this as a "95% confidence interval for the mean". Although our text doesn't use the term "margin of error" explicitly, it seems to me that the margin of error is just the 15.68 term. I've looked at some web sites that define the terms, but there's still some ambiguity - is the margin the range of values or just the half-width of the range? Perhaps that's why our text avoids the issue by not using the term.

Voter Registration and Turnout

Election Data
With the Super Tuesday primaries this past Tuesday, I decided to take a brief look at whatever voting data I could find. I found the Election Assistance Commission web site with data from several past years' elections. I grabbed the 2002 registration and turnout data by state. I'd love to get some more recent data. If you know of a source, please email me or leave a comment.

My initial hypothesis was that registration and turnout should have a pretty strong correlation since, after all, you can't vote if you're not registered. On the other hand, I know that there are some pretty strong voter registration drives with multiple venues for registering, while actual voting is quite controlled and limited in the number of locations where a person can vote. Registration can be highly influenced by outside factors (such as availability and ease of access) while voting itself often needs to be self-motivated.

Here's a plot of the % Register vs. % Turnout by state for the 2002 election:

The coefficient of correlation is 0.382.

Breakdown by Region
Then I thought that perhaps the correlation may be culturally influenced. Could it be that in the northeast states, registration is more closely correlated with voter turnout while in another region the relationship is not as close?

I used the 4 major regions of the US (Northeast, Midwest, South and West) as defined by the US Census Regions and Divisions, and used Minitab to create the plot below:

The regions are:
Northeast 1
Midwest 2
South 3
West 4

I hope to compare the basic descriptive statistics for each region as well as the correlations soon. I do notice some clustering of the data points on cursory inspection.

[Edit] Correlation coefficients by region are:
Northeast: 0.676
Midwest: -0.338
South: 0.063
West: 0.665

How interesting! In the Northeast and West regions, voter turnout is relatively well correlated with registration, while in the South there is little correlation and in the Midwest it's negative! I think a logical next step is to normalize for the total population of each region.

All just food for thought while I wait to get back into the coursework tonight...